本节我们来学习一下压电传感器。

工作原理

压电效应

当某些物质沿某一方向施加压力或拉力时，会产生变形，此时这种材料的两个表面将产生符号相反的电荷。当去掉外力后，它又重新回到不带电状态，此现象称为压电效应。
这种机械能转变为电能的现象，称为“顺压电效应”.
反之，在某些物质的极化方向上施加电场，它会产生机械变形，当去掉外加电场后，该物质的变形随之消失，这种将电能转变为机械能的现象，称为“逆压电效应”

压电常数和表面电荷密度

压电常数是描述材料压电性能的一个重要参数，通常用d表示，单位为库伦/牛顿（C/N）或米/伏（m/V）。它表示在单位力作用下，材料产生的电荷量或在单位电场作用下，材料产生的机械变形量。
我们看这样一个式子，使用单位面积上的电荷量来表示压电效应：

q=\frac{Q}{S}

q=d_{ij}\cdot\sigma=d\cdot\frac{F}{S}

这里对应的物理量分别是：

q为压电元件表面的电荷密度（极化强度），单位：C/cm2；
Q为电荷量，S为受作用力的表面的面积。
d为压电常数，即晶体承受单位作用力时所产生的电荷量，单位：C/N；当受力方向和变形不同时，d也不同。
i=1、2、3——为电荷平面法线方向，即x、y、z轴向；
j= 1、2、3、4、5、6——表示作用力的方向；
σ为作用面上的应力，单位：N/ cm2；
F为作用力；
S为受作用力的表面的面积

压电元件的坐标系表示法

上面描述d_{ij}时提到i和j的取值范围，下面我们来具体了解一下压电元件的坐标系表示法。
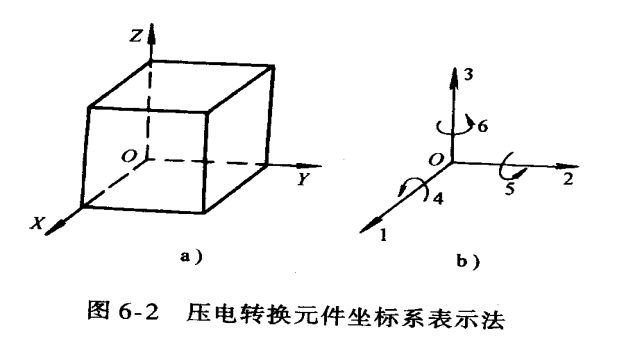
alt text

图中展示了压电元件的坐标系表示法。i=1、2、3分别表示x、y、z轴方向，j=1、2、3分别表示沿x、y、z轴方向的正应力，j=4、5、6分别表示绕x、y、z轴的剪切应力。

这里x、y、z轴有自己对应的名称：

x轴：电轴（通常为晶体的极化方向）；
y轴：机械轴
z轴：光轴

这里的意思也就是说对于一个压电元件来说，它可以在6个不同的方向上受到应力作用，而它在3个不同的方向上产生电荷。d_{ij}中的 i表示电荷产生的方向，j表示应力作用的方向。

压电系数矩阵

如果我们计算各个平面上产生的电荷密度，可以得到下面的矩阵表示法：

\begin{bmatrix} q_1 \\ q_2 \\ q_3 \end{bmatrix}=\begin{bmatrix} d_{11} & d_{12} & d_{13} & d_{14} & d_{15} & d_{16} \\ d_{21} & d_{22} & d_{23} & d_{24} & d_{25} & d_{26} \\ d_{31} & d_{32} & d_{33} & d_{34} & d_{35} & d_{36} \end{bmatrix}\cdot\begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \sigma_4 \\ \sigma_5 \\ \sigma_6 \end{bmatrix}

其中

q_1、q_2、q_3分别表示在x、y、z轴方向上产生的电荷密度；
\sigma_1、\sigma_2、\sigma_3分别表示沿x、y、z轴方向的正应力；
\sigma_4、\sigma_5、\sigma_6分别表示绕x、y、z轴的剪切应力。
d_{ij}表示压电常数矩阵中的元素。

而由d_{ij}组成的矩阵称为压电系数矩阵，它描述了压电元件在不同方向上受到应力作用时产生电荷密度的关系。

例子：石英晶体的压电系数矩阵如下所示：

D=\begin{bmatrix}d_{11}&d_{12}&0&d_{14}&0&0\\0&0&0&0&d_{25}&d_{26}\\0&0&0&0&0&0\end{bmatrix}

这里也就是说，石英晶体在z轴方向上不会产生压电效应。

石英晶体的压电效应

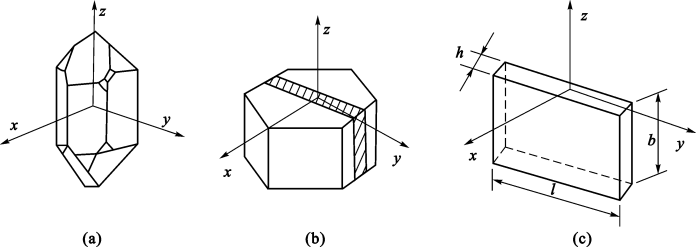
alt text

通常我们如图取石英晶体的一个薄片分析。

压电效应

纵向压电效应

当在x轴方向上施加压力时，晶体会在x轴垂直的两个表面上产生电荷，这就是纵向压电效应。
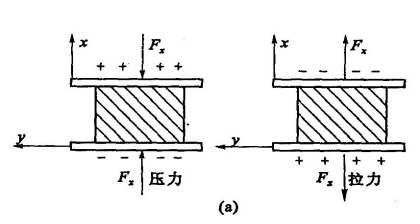
alt text

此时我们可以计算出表面电荷密度为：

q_{11}=d_{11}\cdot\frac{F_{x}}{l\cdot b}

横向压电效应

当在y轴方向上施加压力时：

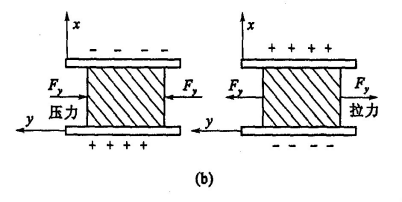
alt text

因为电荷密度（极化强度）

q_{12} = \frac{Q_{12}}{l \cdot b} = d_{12} \cdot \sigma = d_{12} \cdot \frac{F_y}{S} = d_{12} \cdot \frac{F_y}{b \cdot h}

所以

Q_{12} = d_{12} \cdot \frac{F_y \cdot l}{h} = -d_{11} \cdot \frac{F_y \cdot l}{h}

石英晶体的特点

石英晶体是一种天然晶体，它的压电系数为 d_{11}=2.31\times 10^{-12} C/N。莫氏硬度为7，熔点为 1750℃，膨胀系数仅为钢的1/130。

作为常用的压电传感器具有转换效率和转换精度高、线性范围宽、重复性好、固有频率高、动态特性好、工作温度高达550℃（压电系数不随温度而该改变）、工作湿度高达100%等优点，它的稳定性是其他压电材料无法比拟的。

压电陶瓷的压电效应

暂时省略

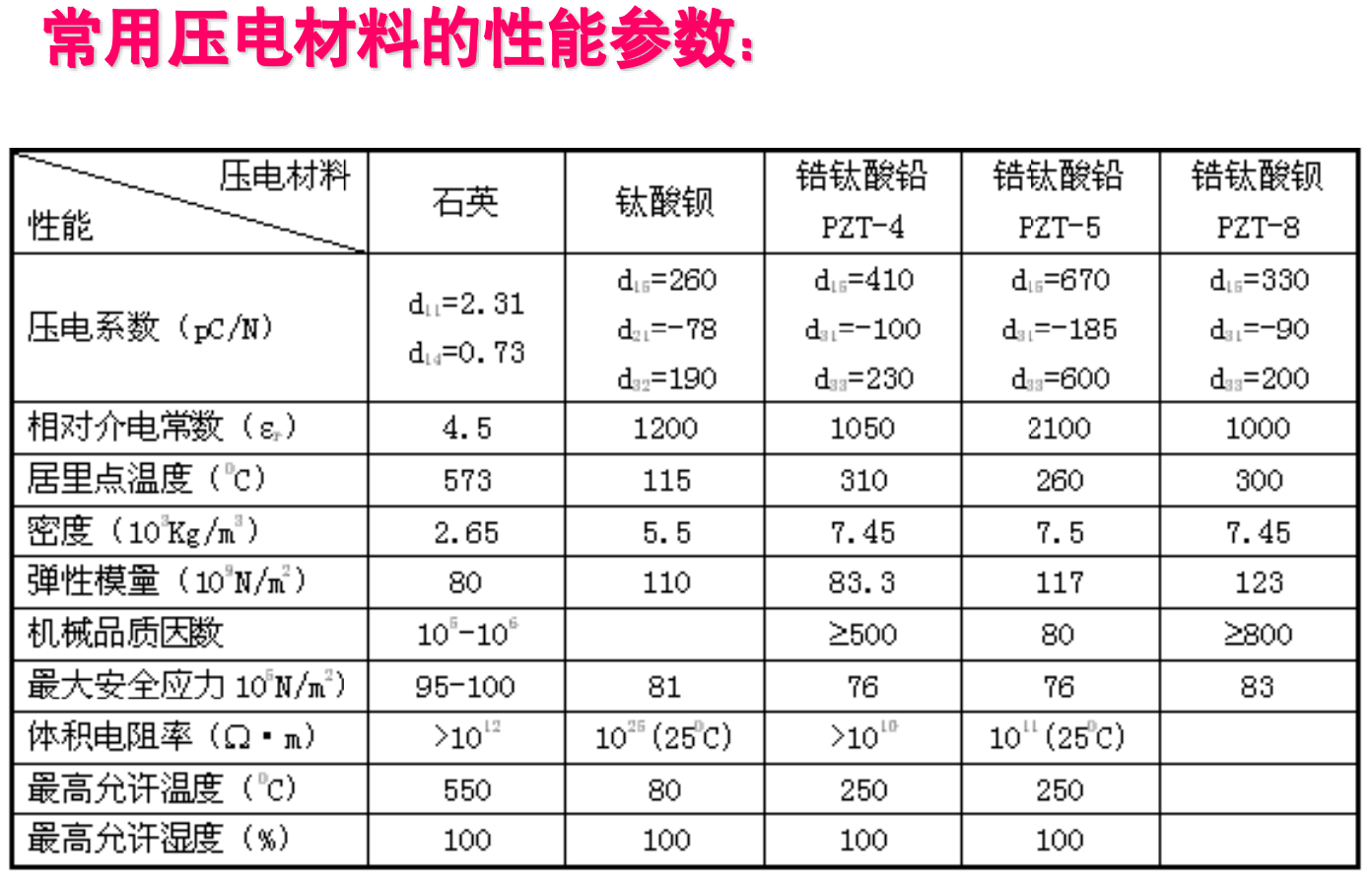
压电材料的主要性能指标

压电系数d：表示压电材料产生电荷与作用力的关系。一般为单位作用力下产生电荷的多少（单位：C/N）。
刚度H：是压电材料的固有频率的重要参数。
介电常数ε：是决定压电晶体固有电容的主要参数，固有电容将影响传感器工作频率的下限值。
电阻R：是压电晶体的内阻，其大小决定泄漏电流。
居里点：即压电效应消失的温度转变点。

alt text

压电传感器的等效和测量电路模型

等效电路模型

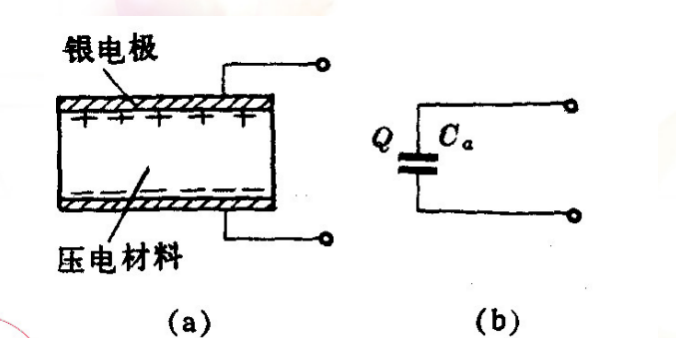
alt text

我们可以把这个视为一个极板电容器,两极板间电压为

U_a=\frac{Q}{C_a}

其负载需要无穷大的输入阻抗R_i，否则会使电荷泄漏，从而影响测量精度。

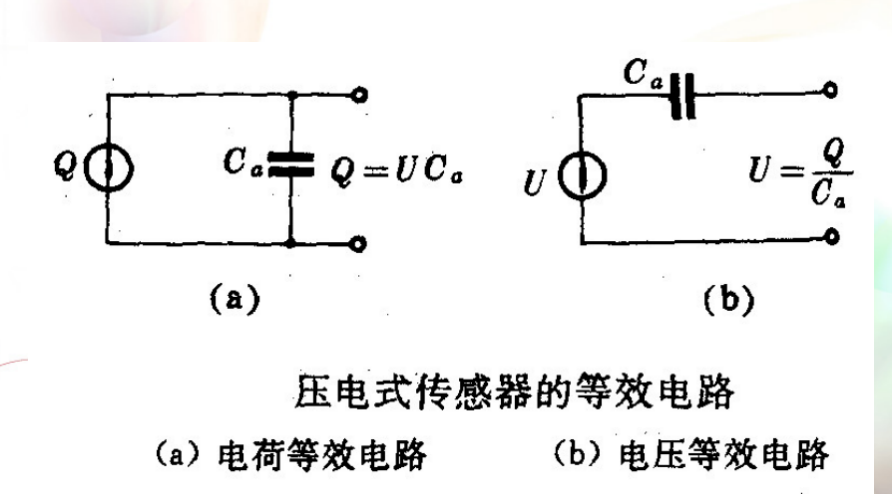
此模型可以根据需要变化：

当需要压电元件输出电荷时，可以把压电元件等效为一个电荷源与一个电容相并联的电荷等效电路。
当需要压电元件输出电压时，可以把压电元件等效为一个电压源与一个电容相串联的电压等效电路。

alt text

测试系统等效电路

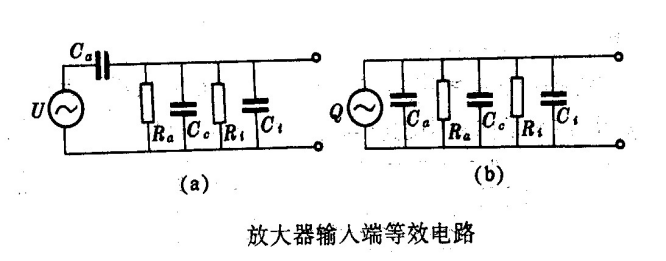
alt text

压电元件的输出信号非常微弱，一般要把其输出信号通过电缆送入前置放大器放大，这样在等效电路中就必须考虑前置放大器的输入电阻、输入电容、电缆电容以及传感器的泄漏电阻（绝缘电阻）。

测量电路

通常将压电传感器的输出信号输入到测量电路的高输入阻抗的前置放大器中来变成低阻抗输出信号，然后再送到测量电路的放大、检波、数据处理电路或显示设备。由此看来，压电传感器的测量电路中的关键部分在前置放大器。

前置放大器有两个作用：

是放大，把压电传感器的微弱信号放大；
是阻抗变换，那传感器的高阻抗输出变换为低阻抗输出。

根据等效电路模型的两种不同形式，前置放大器也有两种不同的连接方式：

电压放大器连接方式
电荷放大器连接方式

电压放大器

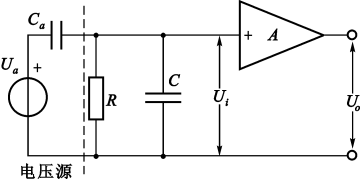
alt text

其中，R和C分别表示前置放大器的等效输入端电阻和等效输入端电容。

R=\frac{R_aR_i}{R_a+R_i}C=C_c+C_i

式中C_{c}代表测量电路联线分布电容（电缆电容），C_{i}代表放大器入端电容。

假设给石英晶体压电元件沿着电轴作用的轴向力为F=F_m\sin \omega t，其压电系数为d_{11}，因此压电效应为Q_a = d_{11}F_m\sin\omega t。
则等效电压源的端电压为u_a=\frac{Q_a}{C_a}=\frac{d_{11}\cdot F_m\sin\omega t}{C_a}

通过电路分析可得前置放大器输出电压为：

\dot U_i =d\cdot\dot{F}\frac{j\omega R}{1+j\omega R(C_a+C)}

然后分析其频率特性：

\left|\frac{U_i}{F}\right|=\frac{d_{11}\cdot R}{\sqrt{1+(\omega R(C_a+C))^2}}

\phi=\tan^{-1}(-\omega R(C_a+C)) + \pi/2

如果当作用在压电元件上的力是静态力，即\omega=0，则前置放大器的输出电压为零。这说明压电传感器不能测量静态力。

设时间常数\tau=R(C_a+C),当\omega \tau>>1时，

U_{im}=\frac{d\cdot F_m\omega R}{\sqrt{1+(\omega\tau)^2}}\doteq\frac{d}{C_a+C}F_m

一般ωτ＞3，上式即可成立，此时说明电压输出型测量电路中的Ui与作用力f的变化频率ω无关，即这种测量电路具有很好高频响应特性，这是其主要优点。此时传感器电压灵敏度为

K_u=\frac{U_{im}}{F_m}=\frac{d}{C_a+C}

电荷放大器

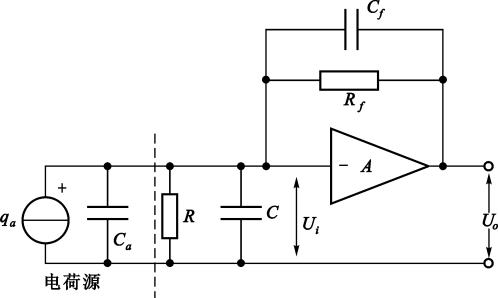
alt text

开环增益A和输入电阻R_i、反馈电阻R_f相当大并视为开路时，放大器的输出电压正比于输入电荷Q。

U_o=-AU_i

\begin{gathered}\text{由于 }U_i=\frac{Q}{C}\quad C=C_a+C_c+C_i+C_f(1+A)\\\text{所以}U_o=-A\frac{Q}{C}=-A\frac{Q}{C_a+C_c+C_i+C_f(1+A)}\\一般A都很大,则C_f(1+A)>>(C_a+Cc+C_f)\\\text{于是}\quad U_0=-\frac{Q}{C_f}\end{gathered}

也就是说，在一定范围内，放大器的输出电压、灵敏度和电缆电容无关，只与反馈电容C_f有关，即和电缆长度无关，这就是电荷放大器的最大优点。