
传感与检测技术:热电偶传感器
热电传感器介绍
在这一章我们来学习热电传感器。热电传感器是一种将温度变化转换为电量变化的装置。它们广泛应用于各种领域,如工业自动化、环境监测和医疗设备等。
热电偶
热电偶是一种常见的热电传感器,由两种不同金属导体组成。当两种金属在不同温度下接触时,会产生电压差,这个现象称为塞贝克效应。热电偶广泛应用于温度测量,具有响应速度快、测量范围广等优点。这将温度变化转换为电压变化,便于测量和控制。
热电阻
热电阻是一种利用材料电阻随温度变化而变化的特性来测量温度的传感器。常见的热电阻材料有铂、镍和铜等。热电阻具有高精度、稳定性好和线性响应等优点,广泛应用于工业过程控制和实验室测量中。也即是将温度变化转换为电阻变化。
在本节,我们主要先介绍热点偶传感器的基本原理
热电偶传感器原理
热电效应
塞贝克效应
塞贝克效应是指当两种不同的导体或半导体在接触点处存在温度差时,会在回路中产生电动势(电压)。这种现象是热电偶传感器工作的基础。热电偶由两种不同金属丝组成,当它们的接点处温度变化时,会产生与温度差成正比的电压。
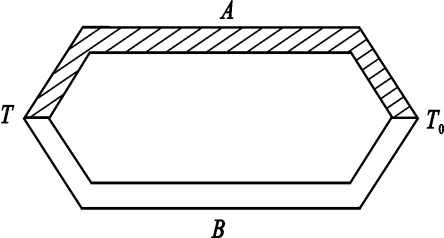
如图所示,热电偶由两种不同金属A和B组成,当接点1和接点2之间存在温度差时,会在回路中产生电动势E。接点1称为热端(T),接点2称为冷端(T_0)。热电偶的输出电压与热端和冷端之间的温度差成正比。
帕尔帖效应
将同温度的两种不同的金属互相接触,由于不同金属内自由电子的密度不同,在它们的接点处会产生接触电动势。
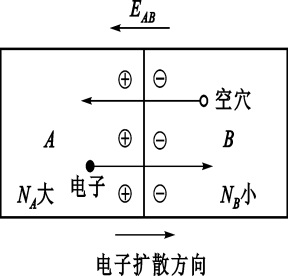
- 热端接触电动势
- 冷端接触电动势
汤姆逊效应
同一种导体在存在温度梯度的情况下,如果有电流通过该导体,则会在导体内部产生热量的吸收或释放现象,两端的温差会引起电动势的产生,这种现象称为汤姆逊效应。
还是看之前那个图片,导体A和B都会各自产生汤姆逊电动势:
- 导体A的汤姆逊电动势
- 导体B的汤姆逊电动势
热电偶的总电动势
由上面三种效应可知,热电偶的总电动势为:
其中,E_{AB}(T)为热端接触电动势,E_{AB}(T_o)为冷端接触电动势,E_A(T-T_o)和E_B(T-T_o)分别为导体A和B的汤姆逊电动势。
不过,汤姆逊效应通常较小,可以忽略不计。因此,热电偶的总电动势简化为:
热电偶的输出电压与热端和冷端之间的温度差成正比,这使得热电偶成为一种有效的温度传感器。当然,上述式子只需要理解原理并且记忆形式即可,实际应用中我们通常使用查表法来获取热电偶的温度与电压之间的关系。
测温原理
热电偶导体A和B材料一定时,回路总电动势成为热端和冷端的温度的函数。在实际测温中,把冷端置于某一恒温下,此时冷端接触电势为一常数,回路总电势仅决定于热端接触电势,即只与热端温度有关,两者之间是单值的函数关系。
即当冷端温度T_0一定时,热电偶的总电动势E_{AB}仅与热端温度T有关,可以表示为:
热电偶的工作特性
基本特性
- 当组成热电偶的两导体性能相同时,则无论接触点处温度如何,热电偶回路总电势为零。
当N_{AT}=N_{BT}且N_{ATo}=N_{BTo}时,有:
这很容易理解,因为此时In\frac{N_{AT}}{N_{BT}}=In\frac{N_{ATo}}{N_{BTo}}=0,所以总电动势为零。
- 当热电偶两接触点处的温度相等时,尽管组成热电偶的两导体材料不同,热电偶回路总电势为零。
当T=T_o时,有:
这也很好理解,因为此时热端和冷端的接触电动势相等,汤姆逊电动势也相等,所以总电动势为零。
那么由上可知,产生回路电动势的充分必要条件是热端和冷端之间存在温度差,并且组成热电偶的两导体材料不同。
也就是:
基本定律
中间导体定律
热电偶回路中间若插入第三种导体C,则只要C的两接触点处温度相等,热电偶回路总电势不变。
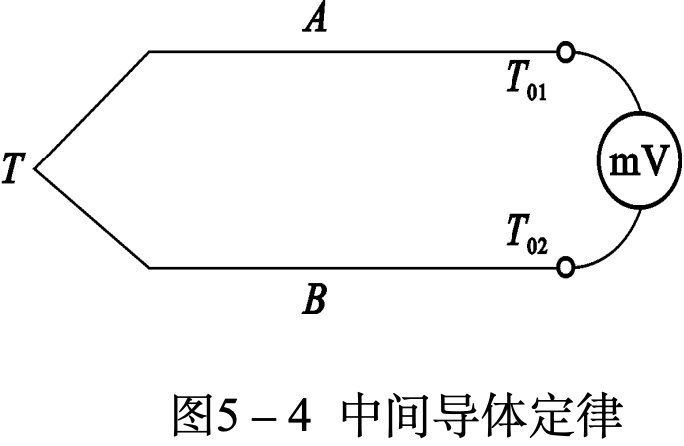
如图,热电偶回路中间插入导体C并且连接毫伏表,当导体C的两接触点处温度相等时,有:
这使得我们在实际测温中可以使用导线将热电偶与测量仪表连接,而不影响测量结果。
标准电极定律
金属A和B之间的电动势等于金属A、C和C、B组成热电偶的热电动势之和。(C为标准电极)
导体C被称为标准电极,通常用纯铂(Pt)作标准电极
中间温度定律
热电偶在接触点温度为T,T_0时的回路电势,等于该热电偶在接触点温度为T,T_n和T_n, T_0时回路电势之代数和。
若T_0=0,则有
现实测量中,冷端温度通常不为零。通常我们使用查分度表法来获取热电偶的温度与电压之间的关系。
比如,我们可以测量的是E_{AB}(T,T_n),然后通过查表获取E_{AB}(T_n,0),最后计算出E_{AB}(T,0),再反查表获取热端温度T。当然,因为分度表只给出了有限的点,我们通常需要进行插值计算。
热点偶冷端补偿
在实际应用中,热电偶的冷端通常无法保持在0℃,而是处于环境温度下。为了准确测量热端温度,需要对冷端温度进行补偿。这一过程称为冷端补偿。并且,分度表通常是以0℃为基准的。
冰浴法
最传统的冷端补偿方法是使用冰浴法。将热电偶的冷端浸入冰水混合物中,保持在0℃,以确保冷端温度恒定。这种方法简单但不便于现场应用。
冷端温度修正法
另一种常用的冷端补偿方法是冷端温度修正法。通过测量冷端的实际温度T_0,然后使用分度表进行修正。具体步骤如下:
- 测量冷端温度T_0,可以使用热电阻或其他温度传感器。
- 读取热电偶的输出电压E_{AB}(T,T_0)。
- 使用分度表查找对应于E_{AB}(T,T_0)的温度T。
- 使用中间温度定律进行修正:
- 最终得到热端温度T。
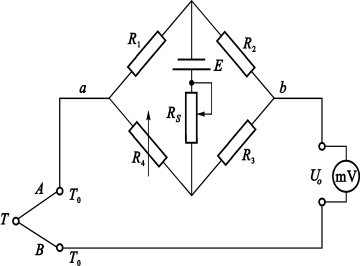
电桥补偿法
利用不平衡电桥产生的电势来补偿热电偶因冷端温度变化而引起的热电势 。
延伸导线法
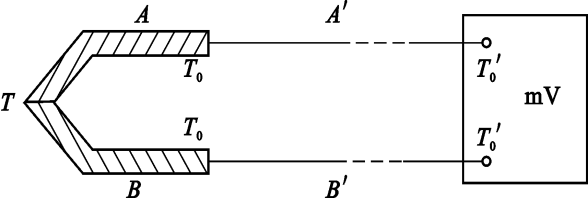
使用与热电偶相同材料(或者是在温度范围内特性相近的材料)制成的延伸导线,将热电偶的冷端连接到测量仪表。这样,延伸导线的接触点温度与冷端温度相同,从而实现冷端补偿。
采用无需补偿的热电偶
某些热电偶材料具有较小的温度系数,在一定温度范围内,其输出电压对冷端温度变化不敏感。这类热电偶可以在无需冷端补偿的情况下使用,但其测量精度可能较低。
如:冷端温度在300℃以下的镍钴—镍铝热电偶,50℃以下的镍铁—镍铜热电偶及铂铑30—铂铑6热电偶
智能补偿
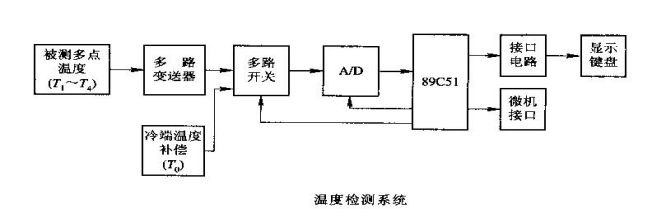
利用单片机或计算机,可以实现温度监测、控制、误差修正与冷端温度补偿一体化和智能化。
总结
热电偶传感器利用塞贝克效应将温度变化转换为电压变化,广泛应用于各种温度测量场合。通过理解热电偶的工作原理、基本特性和冷端补偿方法,可以有效提高测量精度和可靠性。在实际应用中,选择合适的热电偶类型和补偿方法对于确保测量结果的准确性至关重要。
