电阻应变传感器
概述
定义
将被测量的力通过它所产生的金属弹性变形转换成电阻变化的敏感元件。
组成
由弹性元件、电阻应变片和测量电路组成
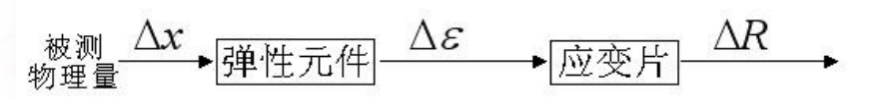
测量原理
工作原理
当金属电阻丝未受力的时候,其原始电阻值为:
R = \rho \frac {L} {S}
当金属丝在外力作用下发生机械变形时,其电阻值将发生变化,这种现象称为金属的电阻应变效应。
我们可以对两端先取对数再求微分:
\frac{\Delta R}{R}=\frac{\Delta L}{L}+\frac{\Delta\rho}{\rho}-\frac{\Delta S}{S}=\frac{\Delta L}{L}+\frac{\Delta\rho}{\rho}-2\frac{\Delta r}{r} \tag{1}
其中将横截面积为圆形的时候,
\frac{\Delta S}{S}=\frac{2\pi r\Delta r}{\pi r^2}=\frac{2\Delta r}{r}
式中\frac{ΔL}{L}是纵向(轴向)变化量,
用应变\mathbf{\varepsilon}表示:
\varepsilon=\frac{\Delta L}L
\frac{\Delta r}r是横向(径向)变化量,用应变\varepsilon_r表示:
\varepsilon_r=\frac{\Delta r}r
由材料力学可知,那么轴向应变和径向应变的
\varepsilon_r=\frac{\Delta r}r=-\mu\frac{\Delta L}L=-\mu\varepsilon
其中\mu 为电阻丝材料的泊松比
将上两式带入(1)得:
\frac{\Delta R}{R}=(1+2\mu)\frac{\Delta L}{L}+\frac{\Delta\rho}{\rho}=(1+2\mu)\varepsilon+\frac{\Delta\rho}{\rho}
电阻丝的灵敏系数定义为单位应变引起的电阻值相对变化
\fcolorbox{red}{#66ccff}{$k_0 = \frac{\Delta R / R}{\varepsilon}$} \\
= (1 + 2\mu) + \frac{\Delta\rho /\rho}{\varepsilon}
对金属丝而言:
\fcolorbox{red}{#66ccff}{$k_0 = 1 + 2\mu$}
当测得应变片电阻值变化量△R时,便可得到被测对象的应变值。往往应变是和应力成正比的。
分类
\text{类型}\begin{cases}\text{金属丝应变片}\\\text{金属电阻应变片}\begin{cases}\text{金属丝应变片}\\\text{金属箔应变片}\\\text{金属薄膜应变片}\end{cases}\\\text{半导体电阻应变片}\end{cases}
按工作温度\begin{cases}\text{常温应变片}&(-30^{\circ}\sim+60^{\circ})\\\text{中温应变片}&(60^{\circ}\sim300^{\circ}C)\\\text{高温应变片}&(300^{\circ}C\text{以上)}\end{cases}
主要特性
1、灵敏系数
K_s=\frac{\Delta R/R}{\varepsilon}
这就是我们之前推导的
2、横向效应
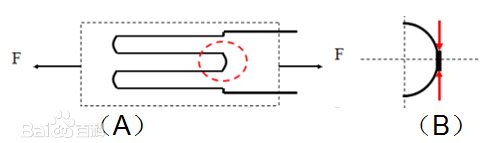
应变片的核心部分是敏感栅。将电阻丝绕成敏感栅后,虽然长度不变,但其直线段和圆弧段的应变状态不同,其灵敏系数K较整长电阻丝的灵敏系数K0小,该现象称为横向效应。
图片来自百度百科,可查看相关词条
3、 机械效应、蠕变、温漂
用于衡量应变片特性对时间的稳定性
- 在恒温下,应变片受力后,其内部会产生不可逆的残余变形,致使应变电阻在加载和卸载时,出现一定的差值,此差值称之为
机械滞后(Hysteresis)
- 应变片受恒定力作用时,应变电阻值随时间而变化,这是因为应力在粘胶层中传递时出现滑动现象,胶层越厚、滑动越严重,这种现象称之为
蠕变
- 温度变化引起应变片电阻值变化的现象称之为
温漂
-
- 由于环境温度改变引起电阻值变化的原因主要有二:
一是电阻丝温度系数引起的;
二是由电阻丝与被测材料的线膨胀系数的不同引起。
4、应变极限和疲劳寿命
应变极限是指在一定温度下,应变片的指示应变与试件的真实应变的相对误差达规定值时的真实应变值。
在恒定幅值的交变力作用下,可以连续工作而不产生疲劳损坏的循环次数N称为应变片的疲劳寿命。
5、绝缘电阻和最大工作电流
绝缘电阻是指已粘贴的应变片的引线与被测件之间的电阻值。通常要求在50~100MΩ以上。
最大工作电流是指已安装的应变片,允许通过敏感栅而不影响其工作特性的最大电流 。通常静态测量时取25mA左右,动态测量时取75~100mA
半导体电阻应变片
半导体应变片是用半导体材料制成的,其工作原理是基于半导体材料的压阻效应。
注意! 这是和金属应变片的不同之处,金属应变片的工作原理是基于金属的应变效应 ,即导体形变引起阻值的变化;而半导体应变片是基于半导体的压阻效应,即半导体电阻率变化引起电阻的变化
1、压阻效应
沿着半导体某晶向施加一定的压力而使其产生应变时其电阻率将随应力改变而变化,这种现象称之为半导体的压阻效应。
2、灵敏系数
\frac {\Delta R} {R} = (1 + 2\mu)\varepsilon + \frac {\Delta \rho} {\rho}
因为 \frac{\Delta\rho}{\rho} \gg (1+2\mu)\varepsilon ,有 \frac{\Delta R}{R} \approx \frac{\Delta\rho}{\rho}
而 \frac{\Delta\rho}{\rho} = \pi E\varepsilon = \pi\sigma
\pi——半导体晶体纵向压阻系数(这里可不是圆周率)
E——半导体晶体弹性模量
所以半导体应变片的纵向压阻效应可由式(2.7)改写为 \frac{\Delta R}{R} = (1+2\mu)\varepsilon + \frac{\Delta\rho}{\rho} \approx \frac{\Delta\rho}{\rho} = \pi E\varepsilon
半导体电阻应变灵敏系数
\fcolorbox{red}{#66ccff}{$ K_B=\frac{\Delta R/R}{\varepsilon}=\frac{\Delta\rho/\rho}{\varepsilon}=\pi E$}
测量电路
工作原理
通常使用电桥法测量。
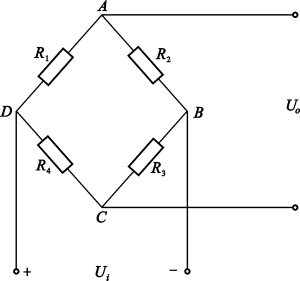
其中R_1和R_2叫做相邻桥臂,R_4和R_3叫做相对桥臂,输入电压U_i,输出电压U_o
测量前,应将电桥调平衡 ,在电桥输出端A和C之间接一检流计调桥臂电阻使检流计指示为0 ,输出电压U0=0,电桥达到平衡状态 。
为了便于分析,一般都取R1=R2=R3=R4=R,称之为等臂桥
单臂法
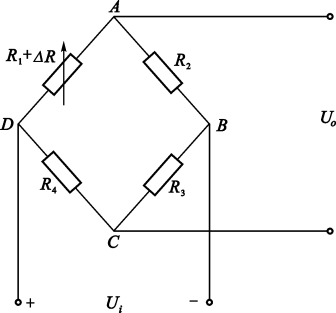
\begin{aligned}&U_O=(\frac{R_1+\Delta R}{R_1+\Delta R+R_2}-\frac{R_4}{R_3+R_4})U_i\\&=(\frac{R+\Delta R}{2R+\Delta R}-\frac{1}{2})U_i\\&=\frac{\Delta R}{2(2R+\Delta R)}U_{i}\\&=\frac{\Delta R/R}{4+2\frac{\Delta R}{R}}U_{i}\\&\approx\frac{\Delta R/R}{4}U_i\\&=\frac{1}{4}K\varepsilon U_i\end{aligned}
这里我们使用了线性近似来得到最后的关系,但本质上这种测量方法得到的输出电压和电阻变化量是非线性的。
我们只需要记忆最后两个式子即可。
单臂电桥的灵敏度(电压灵敏度)
S_u=\frac{U_0}{\Delta R}=\frac{1}{4}U_i
半桥
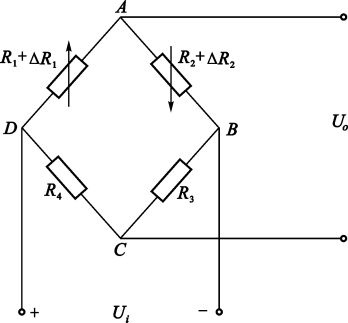
注意这里R1、R2的变化方向是相反的。如果变化方向相同,电桥还是平衡的(即相邻桥臂变化方向相反)
\begin{aligned}&U_{O}=(\frac{R_{1}+\Delta R}{R_{1}+\Delta R+R_{2}-\Delta R}-\frac{R_{4}}{R_{3}+R_{4}})U_{i}\\&=(\frac{R+\Delta R}{2R}-\frac{1}{2})U_{i}\\&=\frac{\Delta R}{2R}U_{i}\\&=\frac{1}{2}K\varepsilon U_{i}\end{aligned}
半桥输出电压和灵敏度都比单臂桥高一倍,并且非线性得到改善。
半桥的灵敏度
S_u=\frac{U_0}{\frac{\Delta R}{R}}=\frac{1}{2}U_i
全桥
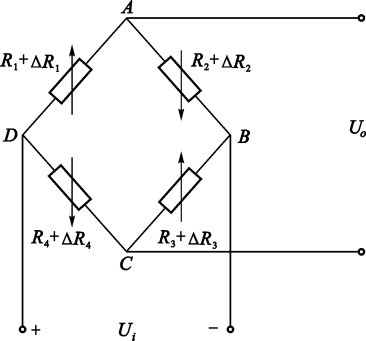
相邻桥臂变化方向相反,相对桥臂变化方向相同
\begin{aligned}&U_{o}=(\frac{R_{1}+\Delta R}{R_{1}+\Delta R+R_{2}-\Delta R}-\\&\frac{R_{4}-\Delta R}{R_{3}+\Delta R+R_{4}-\Delta R})U_{i}\\&=(\frac{R+\Delta R}{2R}-\frac{R-\Delta R}{2R})U_{i}\\&=\frac{2\Delta R}{2R}U_i\\&=K\varepsilon U_{i}\end{aligned}
全桥的灵敏度
S_u=\frac{U_0}{\frac{\Delta R}{R}}=U_i
全桥输出电压和灵敏度又都比半桥高一倍。
应用
应变式力传感器
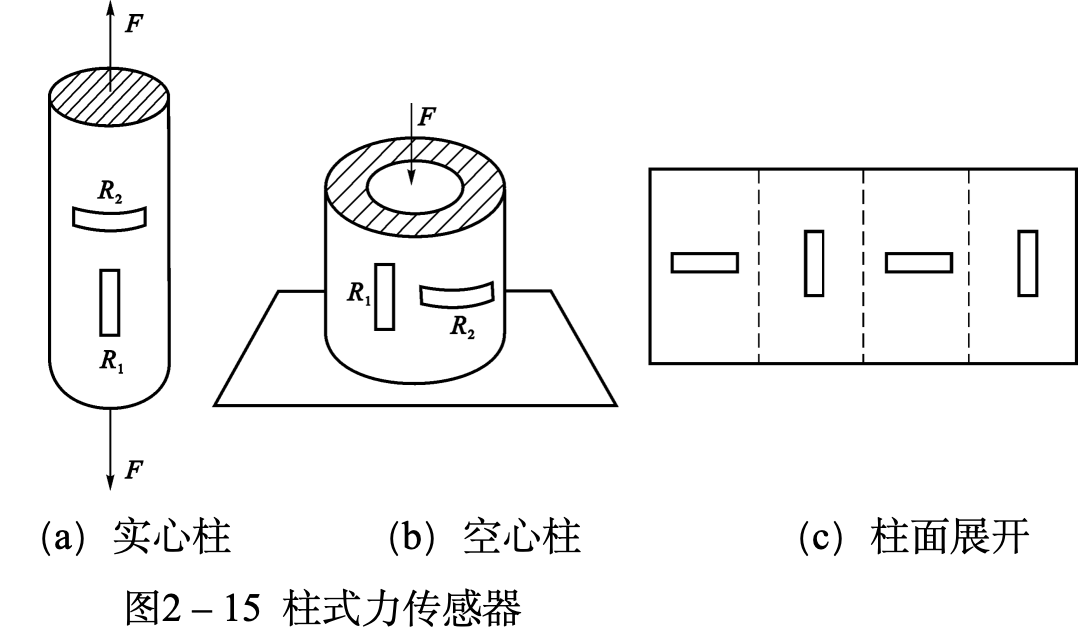
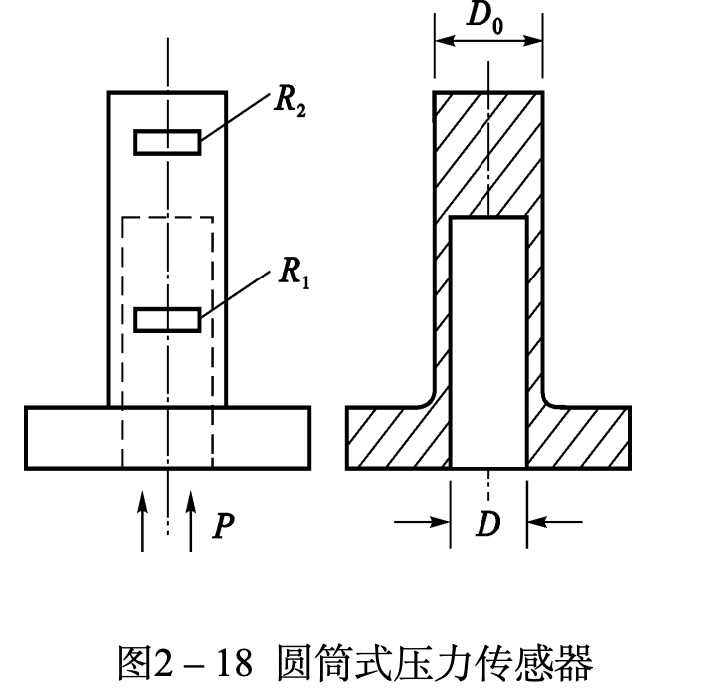
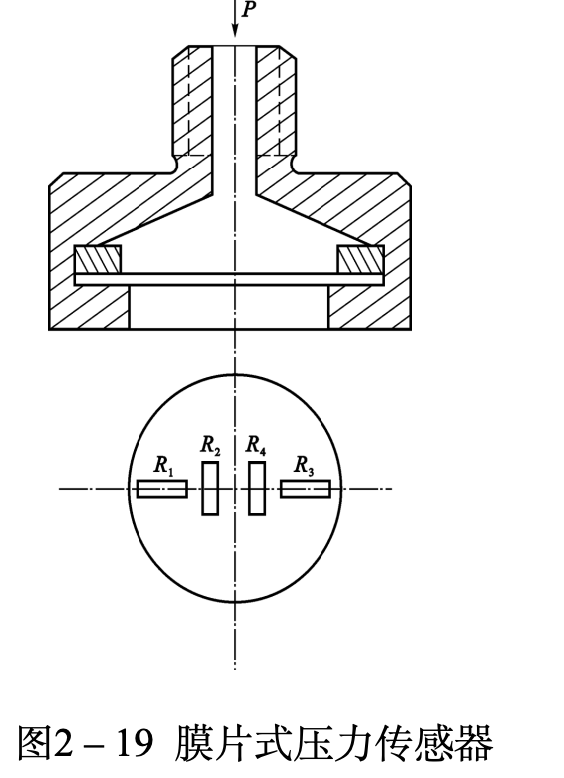
压力传感器