传感和检测技术也进行到第三节课了，由此记一下关于测量误差的笔记

误差的基本概念

绝对误差

即测量值和被测真值间的差值。其中A为真值。常常通过更高一级的仪表得到。

相对误差

实际相对误差

绝对误差与实际值之比

示值相对误差

绝对误差与被测量的的示值之比

引用相对误差

规定量程内的最大绝对误差与测量器具满度值之比

误差的分类

系统误差

在相同条件下，对同一被测量进行多次重复测量时，如果误差按照一定的规律出现，则把这种误差称为系统误差。

检验方法

马利科夫准则

适用于发现线性系统误差。将测量的多次数据按先后次序分为前后两组，然后把两组的残差的代数和相减得到判别之\Delta为：

阿贝-赫梅特准则

适用于周期性系统误差。按先后次序进行排序之后，求出测量列的标准差\hat{\sigma},然后计算统计量

当|C|>\sqrt{n-1}\hat{\sigma}^2时，可认为测量列中含有周期性系统误差

消除方法

引入修正值

由于系统误差的特点是按一定规律变化的，故可引入相应的修正值、修正公式或修正曲线对测量结果进行修正，以减小或消除系统误差。

替代法

用可调的标准量具替代被测量接入检测系统，调整标准量具使检测系统的指示值与被测量接入时相同，此时标准量具的读数就等于被测量。

这里我们就以高中物理中学过的电桥法测量电阻为例子。

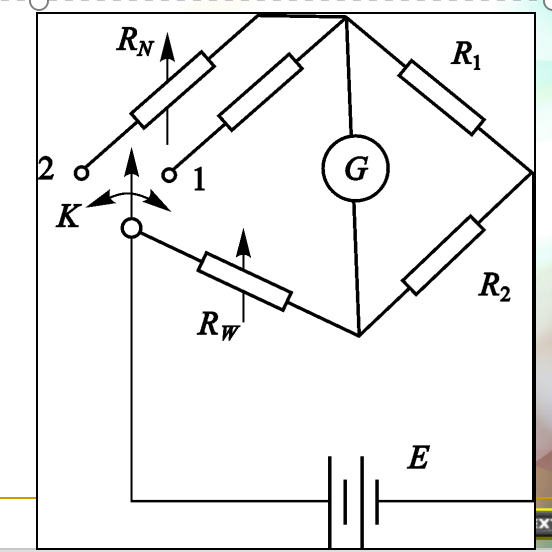
(1) K接1处，调R_{W}，使I_{G}=0，则 R_{x}=\frac{R_{1}}{R_{2}}\cdot R_{W}

(2) 将K换接至2处，调标准量具R_{N}，使I_{G}=0，则 R_{N}=\frac{R_{1}}{R_{2}}\cdot R_{W}

即\textcolor{green}{R_{x}=R_{N}}。

对照法

通过改换被测量在检测电路中的位置而进行两次测量，将两次测量结果进行对照并作相应的数据处理以获得被测量的实际值。被测量仅与标准量具的两次读数有关，而与检测电路无关

我们再来以上面那个电桥测量电阻的例子来说明。如果R_1、R_2我们得到的阻值不是精确的，那么就会产生系统误差。此时我们可以采用下面这种测量方式：

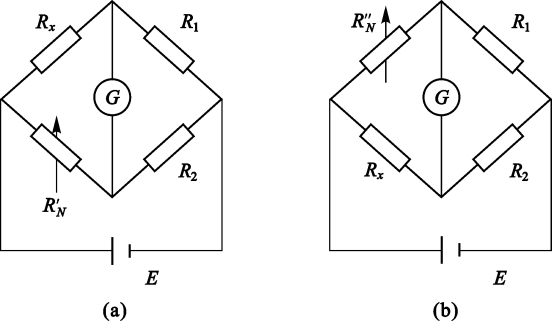
此处我们交换了R_x和R_N位置进行两次测量，根据电桥平衡：

将两个式子相乘，即

随机误差

随机误差的分布特点：

• 对称性 :绝对值相等的正、负误差出现的概率相同。
• 有界性 :绝对值很大的误差几乎不出现。
• 单峰性 :绝对值小的误差出现的概率大于绝对值大的误差出现的概率。
• 抵偿性 : 相同条件下，当测量次数无穷大时，随机误差的代数和趋于零。即正、负随机误差相互抵消。

随机误差往往呈正态分布。说白了其实我们大致上研究的是服从正态分布的随机误差的性质

评价指标

算术平均值（期望）

设对某一量作一系列等精度测量，得到一系列不同的
数值，分别为{X_1},{X_2},{X_3}...{X_N},其算术平均值定义为：

算术平均值接近真值，可以用来代替被测量的真值A_0

均方根误差（方差）

表示随机误差的分布范围、测量数据的精密度。
其计算式为：

• 随机误差 \sigma_{i} = x_{i} - A_{0}
• 剩余误差（残差） v_{i} = x_{i} - \overline{x}
• \sigma 的估计值 \hat{\sigma} = \sqrt{\frac{\sum_{i=1}^{n} v_{i}^{2}}{n-1}} （贝塞尔公式）

如果学习过概率和统计，就会发现实际上 \overline{x} 是对期望的估计， \hat{\sigma} 是对方差的无偏估计。不过前者针对测量的真实值，后者则是针对误差

粗大误差

明显偏离测量结果的误差称为粗大误差。这通常是因为设备、仪器使用不当或者操作人读数问题等等

误差判别

拉伊达准则（3\sigma 准则）

在一组等精度独立测量结果中，其一测量值x_b的残差v_b大于三倍的标准偏差的时候，可能含有粗大误差。当然，3 \sigma法则我们都很熟悉了